Supplemental Material

By ACWE, word polysemy is defined over a latent interpretable semantic space. Each word is represented by one original basic vector over the latent semantic space. Based on the proposed probabilistic model, we can dynamically adjust and update the word vectors based on different contexts to obtain tailored word representations.

Model Inference

The key problem in the inference of a Bayesian graphical model is to estimate the posterior distribution of latent variables conditioned on the observed data. We resort to the variational inference for the model inference. The traditional variational learning method is variational expectation maximization procedure, which requires a full pass through the entire corpus each iteration. One of alternative methods is to consider mini-batches of the data per update to reduce the complexity[1][2][3]. For example, stochastic inference can easily handle data sets of this size and outperforms traditional variational inference shown in [3]. While, the inference process on batches are limited by the arriving of the new words, when our model is trained by stochastic variational inference with a sequence of the mini-batches. Each row of \(\theta\) is the semantic distribution of each word, and the new batch of documents may contain new words whose semantic distribution are never learned. Thus, a tailored stochastic variational algorithm are proposed for the basic word embedding learning to handle the large-scale corpus.

For document \(\mathbf{d}^i\), the fully factorized variational distribution is, $$q^d(\lambda^i, \epsilon^i_j, \{z_l\}^i_j | \xi^i_j, \{\gamma_l\}^i_j) = q(\lambda^i | \rho^i) \prod_{j=1}^{S^i} q(\epsilon^i_j | \xi^i_j) \prod_{l=1}^{N^i_j} q(z^i_{jl} | \gamma^i_{jl}).$$ Thus, the Jensen's lower bound on the log probability of document \(\mathbf{d}^i\) can be computed as: $$ \begin{equation} \begin{split} \mathcal{L}(\rho^i, \xi^i_j, \gamma^i_{jl}; \theta, \beta, \pi, \alpha) &= E[\log p(\lambda^i | \alpha)] + \sum_{j=1}^{S^i} E[\log \epsilon^i_j | \pi] \sum_{j=1}^{S^i} \sum_{l=1}^{N^i_j} E[\log(z^i_{jl} | \vartheta^i_j) ] + \sum_{j=1}^{S^i} \sum_{l=1}^{N^i_j} E[\log p(w^i_{j \cdot l} | z^i_{jl}, \beta_{z^i_{j \cdot l}})] \\ &- E[\log q(\lambda^i | \rho^i)] - \sum_{j=1}^{S^i} E[\log q(\epsilon^i_j | \xi^i_j)] - \sum_{j=1}^{S^i} \sum_{l=1}^{N^i_j} E[\log q(z^i_{jl} | \gamma^i_{jl})], \end{split} \end{equation} $$ where the last three terms indicate the entropies of the variational distributions.

  • Update the variational parameters in the local phase:
    • $$\rho^i_k = \alpha^i_k + \sum_j^{S^i} \sum_l^{N_j^i} \gamma^i_{j\cdot lk} \cdot \frac{\xi^i_{j \cdot (N^i_j +1)}}{\sum_{l^{'}=1}^{N^i_j +1} \xi^i_{j\cdot l^{'}}},$$ $$\gamma^i_{j\cdot lk} \propto \beta_{k,v^{w^i_{j\cdot l}}} \cdot \exp \{ \sum_{l=1}^{N_j^i} \log \theta_{v^{w^i_{j\cdot l}},k} \cdot \frac{\xi^i_{j\cdot l}}{\sum_{l^{'} =1}^{N^i_j +1} \xi^i_{j\cdot l^{'}} } + [\Psi(\rho^i_k) - \Psi(\sum_{k^{'}}^K \rho_{k^{'}}^i)]\frac{\xi^i_{j(N_j^i+1)}}{\sum_{l^{'} =1}^{N^i_j +1} \xi^i_{j\cdot l^{'}}} \},$$ where the subscripts of \([k,v^{w^i_{j\cdot l}}]\) and \([v^{w^i_{j\cdot l}},k]\) denote the corresponding items in matrix \(\beta\) and \(\theta\), respectively. \(\Psi(\cdot)\) indicates the digamma function, the first derivative of the log of the Gamma function. For the attentional signals of words and the host document \(\xi^i_j\) in sentence \(\mathbf{s}^i_j\), we maximize the terms which contain \(\xi\) using gradient descent method as follows: $$ \begin{equation} \begin{split} \mathcal{L}(\xi^i_j) &= \sum_{l^{''}=1}^{N_j^i} \sum_{k=1}^K \gamma^i_{j\cdot l^{''}k} \cdot \left( \sum_{l=1}^{N_j^i} \log \theta_{v^{w^i_{j\cdot l}},k} \cdot \frac{\xi^i_{j\cdot l}}{\sum_{l^{'} =1}^{N^i_j +1} \xi^i_{j\cdot l^{'}} } + [\Psi(\rho^i_k) - \Psi(\sum_{k^{'}}^K \rho_{k^{'}}^i)]\frac{\xi^i_{j(N_j^i+1)}}{\sum_{l^{'} =1}^{N^i_j +1} \xi^i_{j\cdot l^{'}}} \right) \\ &+\sum_{l=1}^{N_j^i+1} (\sum_{l^{'}=1}^{N^i_j +1} \pi_{w^i_{j\cdot l^{'}}} - \xi^i_{j\cdot l})[\Psi(\xi^i_{j\cdot l}) - \Psi(\sum_{l^{'}=1}^{N^i_j +1} \xi^i_{j\cdot l^{'}})] -\log \Gamma(\sum_{l^{'} =1}^{N^i_j +1}\xi^i_{j\cdot l^{'}}) + \sum_{l^{'} =1}^{N^i_j +1}\log \Gamma(\xi^i_{j\cdot l^{'}}). \end{split} \end{equation} $$
  • Update the intermediate global parameters (\(\pi\), \(\alpha\), \(\beta\) and \(\theta\) ) in a mini-batch \(\mathbf{b}\) with \(B\) documents in a iteration:
    • \(\pi\): For the sentence \(\mathbf{s}^i_j\), the involved terms which contain \(\pi\) are: $$\mathcal{L}(\pi_{w^i_j}) = \log \Gamma( \sum_{l=1}^{N_j^i+1}\pi_{w^i_{j\cdot l}}) - \sum_{l=1}^{N_j^i+1} \log \Gamma(\pi_{w^i_{j\cdot l}}) + \sum_{l=1}^{N_j^i+1}(\pi_{w^i_{j\cdot l}} -1)(\Psi(\xi^i_{j\cdot l}) - \Psi(\sum_{l^{'}=1}^{N^i_j +1} \xi^i_{j\cdot l^{'}})).$$ Note that the \(\pi_{w^i_{j\cdot (N_j^i+1)}}\) indicates the \(\pi_{V+1}\) for all sentences.

    \(\alpha\): For each document \(\mathbf{d}^i\), the involved terms which contain \(\alpha\) are: $$\mathcal{L}(\alpha^i) = \log \Gamma(\sum_{k=1}^K \alpha^i_k) - \sum_{k=1}^K \log \Gamma(\alpha^i_k) + \sum_{k=1}^K (\alpha^i_k - 1)(\Psi(\rho^i_k) - \Psi(\sum_{k^{'}=1}^K \rho^i_{k^{'}})).$$ We use gradient descent method by taking derivative of the terms with respect to \(\pi\) and \(\alpha\) to find the estimations of them, respectively. The linear-time Newton-Raphson algorithm can be invoked here.

    \(\beta\): we isolate the corresponding terms and get the following update equation: $$\beta_{kv} \propto \sum_{i=1}^B \sum_{j=1}^{S^i} \sum_{l=1}^{N^i_j} \gamma^i_{j\cdot lk} \cdot (w^i_{jl})^v.$$

    \(\theta\): The update equation of the word embedding matrix \(\theta\) is as follows: $$\theta_{vk} \propto \sum_i^B \sum_j^{S^i} \gamma^i_{j \cdot vk} \cdot \frac{\xi^i_{j, v^{w^i_j}}}{\sum_{l^{'}}^{N^i_j +1} \xi^i_{j\cdot l^{'}}}.$$

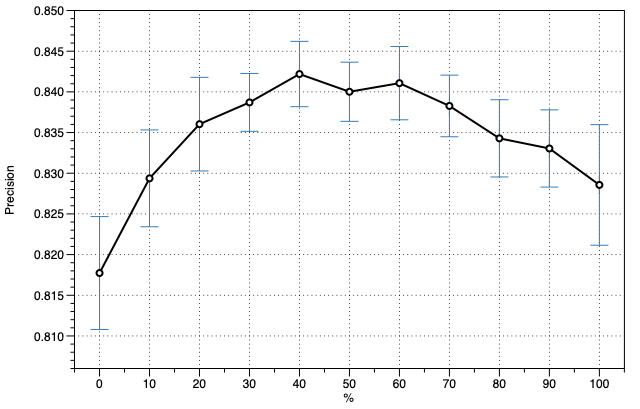
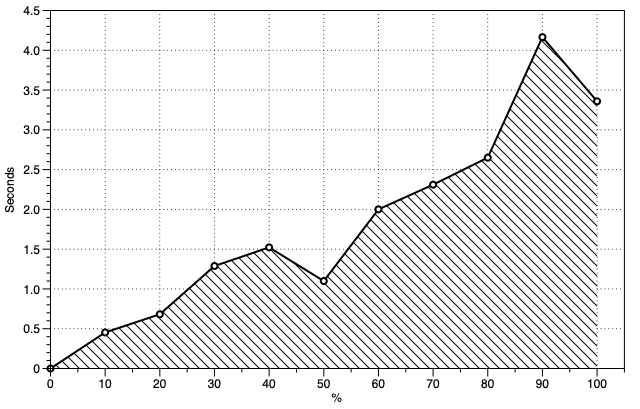
  • Update the current estimate of all the global parameters with the intermediate parameters for the next iteration.

    For \(\theta\), we compute the intermediate global parameter \(\hat{\theta}\) given \(M\) replicates of each document in the \(\mathbf{b}\), and average them in the update: $$ \begin{equation} \hat{\theta}_{vk} \propto \frac{M}{B}\sum_i^B \sum_j^{S^i} \gamma^i_{j \cdot vk} \cdot \frac{\xi^i_{j, v^{w^i_j}}} { \sum_{l^{'}}^{N^i_j +1} \xi^i_{j\cdot l^{'}}}. \tag{1} \end{equation} $$

    Let \(w^b\) denote the unseen words appeared in \(\mathbf{b}\), and \(w_{\_}^b\) indicates the old words which both observed in \(\mathbf{b}\) and the previous mini-batches.

    For \(w^b\), we update the current estimate of the global \(\theta_{w^b}\) with \(\hat{\theta}\) directly.

    For \(w^b_{\_}\), we update \(\theta_{w^b_{\_}}\) using a weighted average of its previous values \(\theta_{w^b_{\_}}\) and the new value \(\theta_{w^b_{\_}}^b\) learned by Eq.(1) in current batch \(\mathbf{b}\). After computing the gradient by \(\nabla \theta_{w^b_{\_}} = \theta_{w^b_{\_}} - \theta_{w^b_{\_}}^b\), we can update \(\theta_{w^b_{\_}}\) following: $$\theta_{w^b_{\_}} = \theta_{w^b_{\_}} - \psi^b \cdot \nabla \theta_{w^b_{\_}} = \theta_{w^b_{\_}} - \psi^b \cdot (\theta_{w^b_{\_}} - \theta_{w^b_{\_}}^b) = (1- \psi^b) \cdot \theta_{w^b_{\_}} + \psi^b \cdot \theta_{w^b_{\_}}^b.$$ where \(\psi^b\) represents the step-size in the iteration of \(\mathbf{b}\). As described in [3], the step-size given to \(\theta_{w^b_{\_}}\) is obtained by, $$\psi^b = (\tau_0 + b)^{-\eta}, \tau_0 \geq 0,$$ where \(\eta \in (0.5,1]\) controls the rate at which old values of \(\theta_{w_{\_}^{b}}\) are forgotten, and the delay \(\tau_0 \geq 0\) down-weights early iterations.

    The \(\beta\) can be updated by, $$ \beta_{vk} = (1- \psi^b) \cdot \beta_{vk} + \psi^b \cdot \frac{M}{B} \sum_{i=1}^B \sum_{j=1}^{S^i} \sum_{l=1}^{N^i_j} \gamma^i_{j\cdot lk} \cdot (w^i_{jl})^v.$$

    We update the current global parameters \(\pi\) and \(\alpha\) as same as \(\beta\).

    • Discussion

    There are two main types of model families to learn word embeddings. One is the type of global matrix factorization methods, such as latent semantic analysis (LSA) and Non-Negative Sparse Embedding (NNSE). The other one is the type of local content window methods, such as the Skip-gram model and the extended models. The proposed ACWE leverages the two types of methods to get the word embeddings. As shown above, ACWE takes advantages of global statistical information to train the original basic word embeddings (see \(\theta\) ), and also, it trains on separate local context windows (sentences) to learn adaptive word embeddings.

    Many current vector-space models of lexical semantics create a single ''prototype'' vector to represent the meaning of a word, or learn multi-prototype word embeddings. Some recent studies attempted to train multi-prototype word embeddings through clustering context window features [4][5], or defining the word embedding number by topics[6][7], or using a specific probability process, such as Chinese restaurant process[8][9]. Differently, ACWE doesn't hold any restricted assumptions for multi-prototype. Each word has an original basic embedding learned from global document information, and an adjusted embedding is generated through the original basic embedding and its present context.

    Comparing with ELMo[10], the word embeddings learned by ACWE are non-negative, because the word embeddings \(\theta\) are generated by a Dirichlet distribution. The non-negative assumption for word embeddings is a good choice for improving the interpretability of word representations described in [11]. The word embeddings learned by ACWE are the semantic distributions over latent interpretable semantics, which is one type of non-negative word embeddings.

    Data and Source Code

    Our code is based on C++ and python 3.5, so the g++ and python are both needed. Click here to download. Here is the version of stochastic variational learning, and Here is the version of online learning.

    We also provide a slice of the preprocessed data from Wikipedia and the labels information.

    Experimental Codes and Results

    You can download all the packages of codes and data to reproduce each part of the experiments, just following the readme.txt contained.

  • Spearman rank correlation

    • Download the codes for Spearman rank correlation.

    Table 1: The results of Spearman rank correlation are in the following table:

    Models WordSim-353 SimLex-999 Rare Word MTruk-771 MEN
    PPMI 0.624 0.241 0.305 0.2950.448
    Sparse Coding 0.596 0.304 0.388 0.3010.476
    CBOW 0.672 0.388 0.452 0.3330.509
    Skip-Gram 0.707 0.361 0.456 0.3520.549
    NNSE 0.686 0.276 0.418 0.3140.492
    GloVe 0.592 0.324 0.341 0.3700.479
    Sparse CBOW 0.670 0.425 0.423 0.3040.518
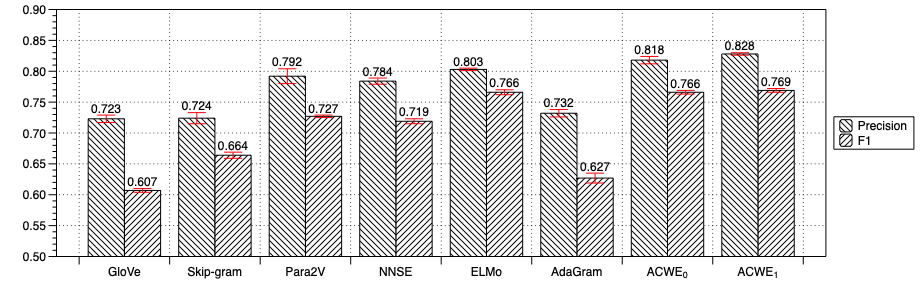
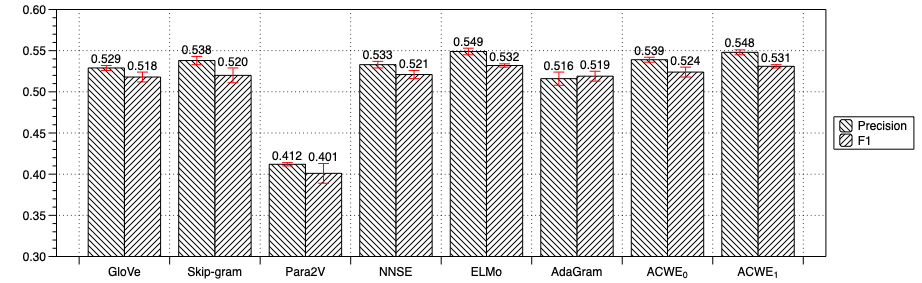
    ACWE 0.713 0.427 0.431 0.3690.550

    Table 2: The results of Spearman correlation coefficient on SCWS with the models which consider word polysemy.
    MP-VSM Multiple-WP PM-MP MSSG TWE NTSG STE ELMo ACWE
    0.594 0.657 0.6360.692 0.681 0.685 0.680 0.703 0.720

  • Similarity of words

    • Download the codes to show similarities of words.

    Following the readme.txt in it, you can test more words ever than the below examples with a simple interactive agent.

    Table 2: Some cases to show the word similarities by raking the top 9 most similar words with cosine distances.

    Words Ranking lists with the corresponding cosine distances
    education (students, 0.99152), (school, 0.99041), (university, 0.98896), (year, 0.98834), (college, 0.98826),
    (post, 0.98798), (report, 0.98790), (public, 0.98774), (teaching, 0.98745)
    China (largest, 0.98666), (Chinese, 0.98556), (Singapore, 0.98455), (united, 0.98433), (Asia, 0.98414),
    (commission, 0.98339), (kingdom, 0.98320), (Russia, 0.98299), (employees, 0.98243)
    movie (music, 0.98738), (stars, 0.98711), (writer, 0.98508), (famous, 0.98484), (film, 0.98470),
    (broadcast, 0.98422), (drama, 0.98416), (song, 0.98402), (actor, 0.98393)
    university (school, 0.99299), (academic, 0.99281), (founded, 0.99255), (students, 0.99236), (college, 0.99211),
    (year, 0.98999), (science, 0.98907), (education, 0.98896), (international, 0.98886)
    programming (computers, 0.98290), (MIT, 0.98193), (intelligence, 0.98180), (implementation, 0.98145),
    (computing, 0.98142), (artificial, 0.981), (technologies, 0.98055), (digital, 0.9805),(communication, 0.9801)

  • Polysemy and interpretability of word embeddings

    • Download the codes to show polysemy and interpretability of word embeddings.

    Following the readme.txt in it, you can test more words ever than the below examples with a simple interactive agent.

    Table 3: The cases to show the word polysemy and interpretability with the top 5 semantics of each word and the top 5 words in each semantic ranked by the log-probabilities.

    Ranking of semantics Ranking of semantics
    county -2.33009 [county, national, historic, located, district]
    -2.787075 [park, river, valley, lake, located]
    -2.986754 [local, authority, city, area, region]
    -3.159863 [south, west, north, east, England]
    -3.184729 [house, historic, style, story, places]    		 teachers -2.575236 [school, year, students, center, community]
    -2.732226 [society, association, members, founded, professional]
    -2.927829 [knowledge, information, management, social, technology]
    -3.521457 [education, centre, college, university, Dr.]
    -3.591531 [people, group, including, world, country]
    collaboration -3.096477 [research, project, institute, foundation, projects]
    -3.221537 [people, group, including, world, country]
    -3.293681 [network, open, access, information, Internet]
    -3.385679 [born, American, January, September, December]
    -3.425838 [development, health, organization, global, European]    		 genomics -1.422867 [biology, molecular, cell, gene, protein]
    -1.610026 [species, evolution, biological, natural, humans]
    -2.701144 [human, theory, study, social, individual]
    -3.071058 [human, brain, mental, cognitive, psychology]
    -3.19488 [concept, terms, object, defined, objects]
    heroes -2.095737 [produced, series, film, films, short]
    -2.755976 [war, army, battle, regiment, navy]
    -3.104434 [American, radio, writer, television, show]
    -3.170857 [Chinese, China, Ng, Beijing, Han]
    -3.315436 [royal,William, son, died, thomas]    		 spectrum -2.463454 [mobile, devices, phone, software, solutions]
    -2.895491 [light, energy, device, speed, motion]
    -3.037028 [molecules, acid, carbon, molecule, compounds]
    -3.191403 [design, power, technology, electronic, equipment]
    -3.372741 [game, playstation, Xbox, nintendo, games]
    template -0.492592 [category, articles, template, automatically, added]
    -2.778984 [page, article, talk, add, Wikiproject]
    -3.872837 [function, distribution, linear, graph, functions]
    -3.969277 [system, systems, developed, based, control]
    -4.108504 [data, processing, applications, information, text]    		 prof -3.045664 [professor, university, science, scientist, computer]
    -3.12606 [university, professor, academic, philosophy, studies]
    -3.262579 [born, American, January, September, December]
    -3.352558 [author, books, science, work, German]
    -3.425612 [people, group, including, world, country]
    papers -3.121343 [journal, peer, reviewed, editor, published]
    -3.132917 [born, American, January, September, December]
    -3.271758 [author, books, science, work, German]
    -3.421435 [book, published, work, English, history]
    -3.453628 [university, professor, academic, philosophy, studies]    		 comedians -2.149376 [television, show, aired, episode, episodes]
    -2.225051 [American, radio, writer, television, show]
    -2.585478 [produced, series, film, films, short]
    -2.797709 [released, series, video, TV, DVD]
    -2.946048 [film, directed, drama, comedy, starring]
    microphones -2.307427 [audio, LG, microphones, tootsie, amplifiers]
    -2.315667 [design, power, technology, electronic, equipment]
    -2.713826 [company, electronics, manufacturer, corporation, market]
    -3.129284 [company, founded, owned, sold, business]
    -3.188213 [mobile, devices, phone, software, solutions]    		 health -2.975491 [care, health, services, hospital, patients]
    -3.141724 [blood, symptoms, risk, vaccine, pregnancy]
    -3.219858 [development, health, organization, global, European]
    -3.27917 [high, includes, including, related, level]
    -3.314238 [medical, medicine, center, health, clinical]
    computers -2.97187 [system, systems, developed, based, control]
    -3.094254 [design, power, technology, electronic, equipment]
    -3.240674 [computer, computing, computers, graphics, dos]
    -3.366713 [mobile, devices, phone, software, solutions]
    -3.406292 [network, open, access, information, Internet]    		 biomedical -2.986134 [research, project, institute, foundation, projects]
    -2.988148 [science, physics, field, scientific, sciences]
    -3.168841 [biology, molecular, cell, gene, protein]
    -3.203789 [human, theory, study, social, individual]
    -3.217035 [medical, medicine, center, health, clinical]

  • Sentence classification tasks by dynamic word embeddings

    • Download the codes to show sentence classification tasks.

    Figure 2: Text classification results for different models with 5-fold cross-validation.

    Figure 3: (Left) Sentence classification results with different ratios on Wikipedia-S. (Right) The average time for each sentence with different ratios.

  • Dynamic word embeddings

    • Download the codes to show Dynamic word embeddings.

    Following the readme.txt in it, you can test more words with different contexts by setting the target word and its context in wordsWithContexts.test file in the downloaded package.

    Table 4: Dynamic word embeddings with different contexts. This above table shows the dynamic embedding changes of “papers” with two different contexts, and the below table shows the word “biomedical”.

    Books or papers printed today, by the same publisher, and from the same type as when they were first published, are still the first editions of these books to a bibliographer. I know of a research group in a university where students submit some academic papers without their professor having read them, let alone contributing to the work.
    -0.140819 [published, book, written, wrote, edition]
    -2.286497 [journal, peer, reviewed, scientific, academic]
    -3.945425 [type, volume, frequently, visual, notably]
    -5.231559 [included, magazine, leading, editor, press]
    -6.079971 [records, record, index, literature, reference]    		 -0.823609 [research, project, foundation, led, projects]
    -1.037011 [journal, peer, reviewed, scientific, academic]
    -2.664416 [university, professor, faculty, Harvard, department]
    -3.089699 [field, study, studies, scientific, fields]
    -3.266090 [students, student, teaching, teachers, teacher]
    Biomedical definition, the application of the natural sciences, especially the biological and physiological sciences, to clinical medicine. The treatments available at biomedical Center include natural herbs, special diet, vitamins and minerals, lifestyle counseling, positive attitude, and conventional medical treatments when indicated.
    -1.009875 [field, study, studies, scientific, fields]
    -1.171692 [biology, molecular, biological, genetics, ecology]
    -2.172841 [medical, medicine, clinical, patient, surgery]
    -2.231589 [institute, established, centre, private, institution]
    -3.357441 [science, fellow, MIT, Stanford, laboratory]    		 -0.826321 [center, Massachusetts, Boston, Dr., Md.]
    -0.864242 [medical, medicine, clinical, patient, surgery]
    -2.540809 [include, applications, processing, large, techniques]
    -3.798415 [natural, areas, land, environmental, environment]
    -4.364615 [disease, treatment, effects, cancer, risk]
    Light is electromagnetic radiation within a certain portion of the electromagnetic spectrum. A railbus is a light weight passenger rail vehicle that shares many aspects of its construction with a bus. Heavy weights are good for developing strength and targeting specific muscle, and light weights are good for build and maintain lean muscle.
    --0.129370 [nuclear, light, radiation, magnetic, experiments]
    -3.438747 [term, refers, word, meaning, means]
    -3.585760 [image, images, color, vision, camera]
    -3.752776 [line, station, railway, operated, bus]
    -4.770996 [energy, mass, particles’, electron, atomic]    		 -0.440478 [line, station, railway, operated, bus]
    -1.815225 [body, exercise, lower, weight, strength]
    -2.777080 [process, single, typically, multiple, result]
    -3.266629 [original, play, stage, theatre, tragedy]
    -4.287032 [construction, formed, cross, bridge, replaced]     		-1.226888 [common, specific, terms, concept, object]
    -1.251034 [body, exercise, lower, weight, strength]
    -2.309753 [cell, cells, blood, growth, muscle]
    -2.868760 [process, single, typically, multiple, result]
    -2.941860 [due, high, low, quality, additional]

    [1] Bottou, Léon, and Olivier Bousquet. "The tradeoffs of large scale learning." Advances in neural information processing systems. 2008.

    [2] Liang, Percy, and Dan Klein. "Online EM for unsupervised models." Proceedings of human language technologies: The 2009 annual conference of the North American chapter of the association for computational linguistics. 2009.

    [3] Hoffman, Matthew D., et al. "Stochastic variational inference." The Journal of Machine Learning Research 14.1 (2013): 1303-1347.

    [4] Reisinger, Joseph, and Raymond J. Mooney. "Multi-prototype vector-space models of word meaning." Human Language Technologies: The 2010 Annual Conference of the North American Chapter of the Association for Computational Linguistics. Association for Computational Linguistics, 2010.

    [5] Huang, E. H., Socher, R., Manning, C. D., & Ng, A. Y. (2012, July). Improving word representations via global context and multiple word prototypes. In Proceedings of the 50th Annual Meeting of the Association for Computational Linguistics: Long Papers-Volume 1 (pp. 873-882). Association for Computational Linguistics.

    [6] Liu, Y., Liu, Z., Chua, T. S., & Sun, M. (2015, February). Topical word embeddings. In Twenty-Ninth AAAI Conference on Artificial Intelligence.

    [7] Liu, P., Qiu, X., & Huang, X. (2015, June). Learning context-sensitive word embeddings with neural tensor skip-gram model. In Twenty-Fourth International Joint Conference on Artificial Intelligence.

    [8] Neelakantan, A., Shankar, J., Passos, A., & McCallum, A. (2015). Efficient non-parametric estimation of multiple embeddings per word in vector space. arXiv preprint arXiv:1504.06654.

    [9] Bartunov, S., Kondrashkin, D., Osokin, A., & Vetrov, D. P. (2016, May). Breaking Sticks and Ambiguities with Adaptive Skip-gram. In AISTATS (pp. 130-138).

    [10] Peters, M. E., Neumann, M., Iyyer, M., Gardner, M., Clark, C., Lee, K., & Zettlemoyer, L. (2018). Deep contextualized word representations. arXiv preprint arXiv:1802.05365.

    [11] Luo, H., Liu, Z., Luan, H., & Sun, M. (2015). Online learning of interpretable word embeddings. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing (pp. 1687-1692).